What are the chances that twins are a) two girls, b) two boys, or c) a boy and a girl?
Try it by tossing two coins.
Two girls: ¼, two boys: ¼, a girl and a boy: ½.
www.sciensation.org | Ciênsação hands-on experiments are published as Open Educational resources under a Creative Commons Attribution-ShareAlike 4.0 International License.
What are the chances that twins are a) two girls, b) two boys, or c) a boy and a girl?
Try it by tossing two coins.
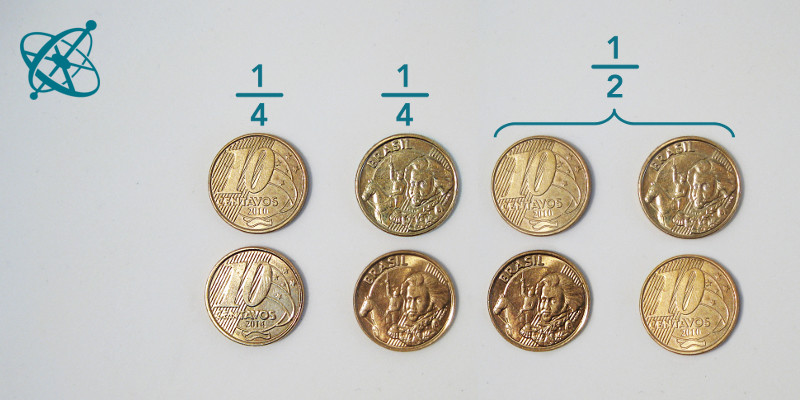
Two girls: ¼, two boys: ¼, a girl and a boy: ½.
Heads 'n tails
A woman gives birth to fraternal twins: what is the probability that they are a) two girls, b) two boys, or c) a boy and a girl?
You might think that the answer is obvious, but surprisingly many people hold on to a misconception: Since there are three possible outcomes listed, each has a probability of 1/3. Even if you explain that the third option actually encompasses two possible outcomes (boy + girl, girl + boy), words alone won't really convince everyone. A brief experiment, on the other hand...
Addressing a common misconception in the perception of probabilities.
Discuss with your students if it is more likely for a woman with fraternal twins, i.e. developed from two different eggs, to have a) two girls, b) two boys c) a boy and a girl, or if d) all three possibilities are equally likely.
If you note that some students are tending to option D, make the class do an experiment with coin tosses. Prepare a table on the whiteboard to record your students' results.
Toss two coins and report if you got two heads, two tails or a head and a tail.
Are 'boy+girl' and 'girl+boy' the same outcome?
› For the parents yes, but to calculate the probability correctly, they need to be considered as two distinct cases.
Since 'head+tail' and 'tail+head' are indistinguishable, the combination of head and tail occurs about twice as often as 'head+head' or 'tail+tail'.