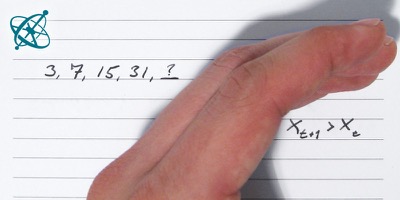Next comes 63 – double the last number and add 1, right?
63 is right, but the rule is not. It is far simpler.
How to discover the rule with as little attempts as possible?
www.sciensation.org | Ciênsação hands-on experiments are published as Open Educational resources under a Creative Commons Attribution-ShareAlike 4.0 International License.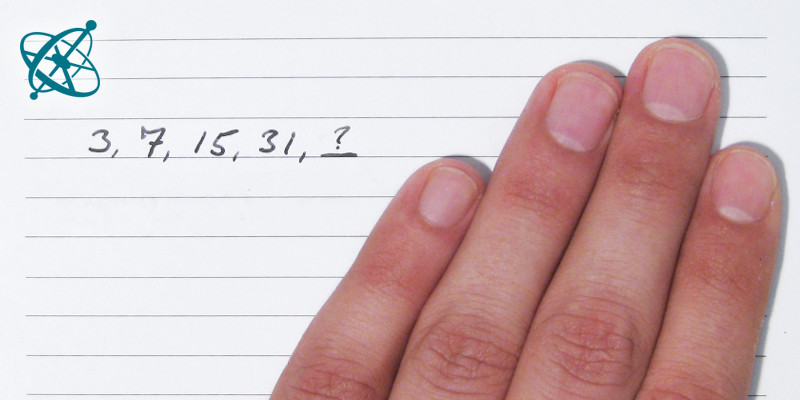
Next comes 63 – double the last number and add 1, right?
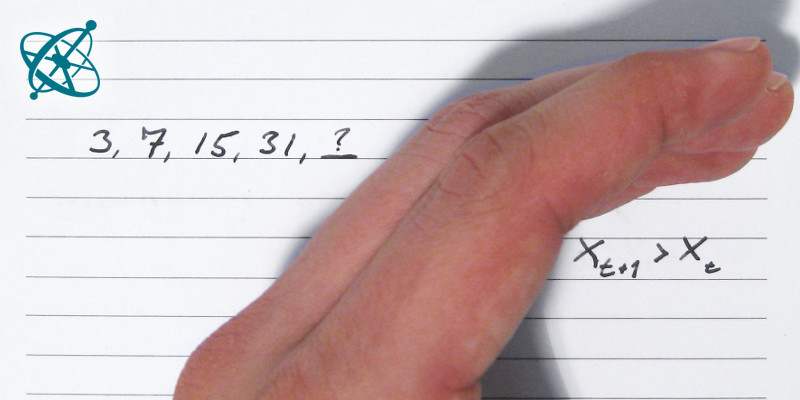
63 is right, but the rule is not. It is far simpler.
How to discover the rule with as little attempts as possible?
Guess my rule – like a scientist
This little game is based on a famous psychology experiment. Researchers demonstrated with it that humans often hold a confirmation bias: We naturally tend to seek evidence that confirms our current believes, rather than to look for evidence that falsifies theories.
Karl Popper, one of the most influential philosophers of science in the 20th century, argued that a single experiment can falsify a theory, but no number of experiments confirming a theory can exclude the possibility that the theory is wrong. He concluded that one should scrutinize all scientific theories by searching decisive experiments to falsify them.
Motivated by the context of a game, your students will find that this approach indeed is an effective strategy to win – both in this game and in science.
Fostering analytical thinking.
Realizing and ideally overcoming confirmation bias.
Applying the scientific method efficiently.
Write on the whiteboard a series of numbers according to the simple rule that each number has to be larger than the previous one, e.g. 3, 7, 15, 31,... Then challenge your students to discover the rule you used. They can ask if a specific number is a valid continuation of the series or not, upon which you only answer with 'yes' or 'no'. Write down each test number and your answer on the whiteboard. When they are sure they know your rule, let them guess it, but give them a maximum of 3 attempts.
After you discussed with them advantages and disadvantages of different strategies, give them a second chance to apply what they learned, e.g. by using the rule that the difference between consecutive numbers has to be larger than 10.
Find the rule your teacher uses to generate the series of numbers. You can ask your teacher if a certain number is a valid continuation or not.
When you try to discover the rule, is it more efficient to ask for numbers that confirm or that falsify the rule you have in mind?
› An answer that allows to exclude a wrong rule is better than one that may or may not mean that your hypothesis is right. Probing numbers to falsify possible rules are therefore more efficient.
An effective strategy for finding the underlying rule with a minimum of trials: Think of possible rules and test them by naming numbers that would falsify them. Start with the simplest rule, and then exclude rules until the remaining option appears sufficiently tested to be used as a guess.
After your students understood this concept, show them how it is applied in different sciences.